Put in Order From Least to Greatest Put in Order From Least to Greatest Clip Art

Largest positive integer that divides two or more integers

In mathematics, the greatest common divisor (GCD) of ii or more integers, which are not all zero, is the largest positive integer that divides each of the integers. For two integers x, y, the greatest common divisor of x and y is denoted $\gcd(x,y)$ . For example, the GCD of eight and 12 is 4, that is, $\gcd(8,12)=iv$ .^[1] ^[ii]

In the name "greatest common divisor", the adjective "greatest" may be replaced by "highest", and the give-and-take "divisor" may be replaced by "factor", then that other names include highest common factor (hcf), etc.^[3] ^[4] ^[5] ^[6] Historically, other names for the same concept take included greatest common mensurate.^[7]

This notion can be extended to polynomials (meet Polynomial greatest common divisor) and other commutative rings (see § In commutative rings beneath).

Overview [edit]

Definition [edit]

The greatest mutual divisor (GCD) of two nonzero integers $a$ and $b$ is the greatest positive integer $d$ such that $d$ is a divisor of both $a$ and $b$ ; that is, there are integers $e$ and $f$ such that $a = de$ and $b = df$ , and $d$ is the largest such integer. The GCD of $a$ and $b$ is generally denoted $gcd(a, b)$ .^[viii]

This definition too applies when one of $a$ and $b$ is zero. In this instance, the GCD is the absolute value of the not naught integer: $gcd(a, 0) = gcd(0, a) = | a |$ . This case is important as the terminating footstep of the Euclidean algorithm.

The above definition cannot exist used for defining $gcd(0, 0)$ , since $0 \times n = 0$ , and zero thus has no greatest divisor. Still, zero is its own greatest divisor if greatest is understood in the context of the divisibility relation, so $gcd(0, 0)$ is usually defined as 0. This preserves the usual identities for GCD, and in detail Bézout'south identity, namely that $gcd(a, b)$ generates the same platonic as ${a, b}$ .^[9] ^[x] ^[11] This convention is followed by many calculator algebra systems.^[12] Nonetheless, some authors leave $gcd(0, 0)$ undefined.^[13]

The GCD of $a$ and $b$ is their greatest positive mutual divisor in the preorder relation of divisibility. This means that the common divisors of $a$ and $b$ are exactly the divisors of their GCD. This is commonly proved by using either Euclid's lemma, the fundamental theorem of arithmetics, or the Euclidean algorithm. This is the meaning of "greatest" that is used for the generalizations of the concept of GCD.

Case [edit]

The number 54 can be expressed as a product of two integers in several different ways:

54\times one=27\times 2=18\times 3=9\times six.

Thus the complete listing of divisors of 54 is $1,2,3,vi,ix,eighteen,27,54$ . Similarly, the divisors of 24 are $ane,2,iii,iv,6,eight,12,24$ . The numbers that these ii lists have in mutual are the common divisors of 54 and 24, that is,

i,2,iii,half dozen.

Of these, the greatest is 6, so it is the greatest common divisor:

\gcd(54,24)=6.

Calculating all divisors of the ii numbers in this mode is ordinarily not efficient, peculiarly for big numbers that accept many divisors. Much more efficient methods are described in § Calculation.

Coprime numbers [edit]

Two numbers are called relatively prime number, or coprime, if their greatest common divisor equals 1.^[xiv] For example, 9 and 28 are Coprime.

A geometric view [edit]

A 24-past-60 rectangle is covered with x 12-by-12 square tiles, where 12 is the GCD of 24 and lx. More generally, an a-by-b rectangle can be covered with square tiles of side length c only if c is a common divisor of a and b.

For example, a 24-by-60 rectangular area can be divided into a grid of: 1-past-1 squares, two-past-2 squares, iii-past-three squares, 4-by-iv squares, six-by-six squares or 12-by-12 squares. Therefore, 12 is the greatest common divisor of 24 and 60. A 24-past-60 rectangular surface area can thus be divided into a grid of 12-by-12 squares, with two squares along one border (24/12 = ii) and five squares along the other (threescore/12 = 5).

Applications [edit]

Reducing fractions [edit]

The greatest mutual divisor is useful for reducing fractions to the lowest terms.^[15] For example, gcd(42, 56) = 14, therefore,

{\frac {42}{56}}={\frac {iii\cdot 14}{four\cdot xiv}}={\frac {3}{4}}.

Least mutual multiple [edit]

The least mutual multiple of two integers that are not both aught can be computed from their greatest mutual divisor, by using the relation

\operatorname {lcm} (a,b)={\frac {|a\cdot b|}{\operatorname {gcd} (a,b)}}.

Adding [edit]

Using prime factorizations [edit]

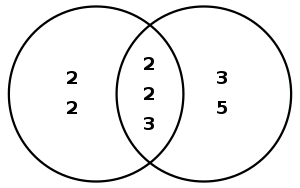
Greatest mutual divisors tin exist computed by determining the prime factorizations of the ii numbers and comparing factors. For example, to compute gcd(48, 180), we find the prime factorizations 48 = 2^iv · 3¹ and 180 = two² · iii² · five¹; the GCD is then 2^min(4,2) · 3^min(1,2) · 5^min(0,1) = ii² · iii¹ · five⁰ = 12, as shown in the Venn diagram. The respective LCM is then 2^max(4,2) · iii^max(1,two) · five^max(0,one) = 2⁴ · 3² · five^one = 720.

^[16]

In practice, this method is simply viable for small numbers, every bit calculating prime number factorizations takes too long.

Euclid's algorithm [edit]

The method introduced past Euclid for computing greatest mutual divisors is based on the fact that, given 2 positive integers $a$ and $b$ such that $a > b$ , the mutual divisors of $a$ and $b$ are the same every bit the common divisors of $a - b$ and $b$ .

So, Euclid'southward method for computing the greatest common divisor of two positive integers consists of replacing the larger number by the difference of the numbers, and repeating this until the 2 numbers are equal: that is their greatest common divisor.

For example, to compute $gcd(48,18)$ , i gain equally follows:

{\begin{aligned}\gcd(48,xviii)\quad &\to \quad \gcd(48-18,18)=\gcd(30,18)&&\to \quad \gcd(xxx-xviii,18)=\gcd(12,18)\\&\to \quad \gcd(12,18-12)=\gcd(12,6)&&\to \quad \gcd(12-vi,vi)=\gcd(6,6).\cease{aligned}}

So $gcd(48, 18) = 6$ .

This method can exist very slow if ane number is much larger than the other. So, the variant that follows is mostly preferred.

Euclidean algorithm [edit]

Animation showing an application of the Euclidean algorithm to find the greatest mutual divisor of 62 and 36, which is 2.

A more than efficient method is the Euclidean algorithm, a variant in which the divergence of the ii numbers $a$ and $b$ is replaced by the residue of the Euclidean division (also chosen sectionalization with balance) of $a$ by $b$ .

Denoting this residuum every bit $a mod b$ , the algorithm replaces $(a, b)$ by $(b, a mod b)$ repeatedly until the pair is $(d, 0)$ , where $d$ is the greatest mutual divisor.

For instance, to compute gcd(48,18), the computation is as follows:

{\begin{aligned}\gcd(48,xviii)\quad &\to \quad \gcd(18,48{\bmod {1}}8)=\gcd(18,12)\\&\to \quad \gcd(12,eighteen{\bmod {1}}2)=\gcd(12,half-dozen)\\&\to \quad \gcd(6,12{\bmod {vi}})=\gcd(six,0).\terminate{aligned}}

This again gives $gcd(48, 18) = half-dozen$ .

Lehmer'southward GCD algorithm [edit]

Lehmer's algorithm is based on the observation that the initial quotients produced past Euclid's algorithm tin can exist determined based on only the first few digits; this is useful for numbers that are larger than a reckoner word. In essence, one extracts initial digits, typically forming 1 or two computer words, and runs Euclid's algorithms on these smaller numbers, equally long every bit it is guaranteed that the quotients are the same with those that would be obtained with the original numbers. The quotients are nerveless into a modest ii-by-2 transformation matrix (a matrix of single-discussion integers) to reduce the original numbers. This process is repeated until numbers are small enough that the binary algorithm (see beneath) is more efficient.

This algorithm improves speed, because it reduces the number of operations on very large numbers, and tin can use hardware arithmetic for nigh operations. In fact, most of the quotients are very modest, so a fair number of steps of the Euclidean algorithm can be collected in a two-by-2 matrix of unmarried-give-and-take integers. When Lehmer's algorithm encounters a caliber that is too large, it must fall dorsum to ane iteration of Euclidean algorithm, with a Euclidean sectionalisation of large numbers.

Binary GCD algorithm [edit]

The binary GCD algorithm uses only subtraction and division by two. The method is equally follows: Let a and b be the two non-negative integers. Let the integer d be 0. There are five possibilities:

a = b.

As gcd(a, a) = a, the desired GCD is a × 2^d (as a and b are changed in the other cases, and d records the number of times that a and b have been both divided past ii in the next step, the GCD of the initial pair is the product of a and two^d).

Both a and b are even.

And so 2 is a common divisor. Divide both a and b past 2, increment d past 1 to record the number of times 2 is a common divisor and proceed.

a is even and b is odd.

And so 2 is non a common divisor. Divide a by ii and proceed.

a is odd and b is even.

Then 2 is not a common divisor. Divide b by ii and keep.

Both a and b are odd.

As gcd(a,b) = gcd(b,a), if a < b then substitution a and b. The number c = a − b is positive and smaller than a. Any number that divides a and b must also split up c so every common divisor of a and b is also a common divisor of b and c. Similarly, a = b + c and every mutual divisor of b and c is also a mutual divisor of a and b. So the two pairs (a, b) and (b, c) have the same common divisors, and thus gcd(a,b) = gcd(b,c). Moreover, as a and b are both odd, c is even, the process can exist continued with the pair (a, b) replaced by the smaller numbers (c/2, b) without changing the GCD.

Each of the above steps reduces at least one of a and b while leaving them non-negative and and then tin can only be repeated a finite number of times. Thus eventually the process results in a = b, the stopping case. So the GCD is a × 2^d.

Example: (a, b, d) = (48, eighteen, 0) → (24, ix, 1) → (12, 9, 1) → (6, 9, 1) → (3, 9, one) → (3, 3, one) ; the original GCD is thus the product vi of ii^d = 2¹ and a= b= 3.

The binary GCD algorithm is particularly piece of cake to implement on binary computers. Its computational complexity is

O((\log a+\log b)^{ii})

The computational complexity is usually given in terms of the length $n$ of the input. Here, this length is $n=\log a+\log b,$ and the complexity is thus

O(due north^{2})

Other methods [edit]

$\gcd(one,x)=y,$ or Thomae'southward function. Hatching at lesser indicates ellipses (i.e. omission of dots due to the extremely loftier density).

If a and b are both nonzero, the greatest common divisor of a and b can be computed by using least common multiple (LCM) of a andb:

\gcd(a,b)={\frac {|a\cdot b|}{\operatorname {lcm} (a,b)}}

but more usually the LCM is computed from the GCD.

Using Thomae'due south function f,

\gcd(a,b)=af\left({\frac {b}{a}}\right),

which generalizes to a and b rational numbers or commensurable existent numbers.

Keith Slavin has shown that for odd a ≥ ane:

\gcd(a,b)=\log _{two}\prod _{k=0}^{a-1}(1+east^{-2i\pi kb/a})

which is a function that tin can exist evaluated for circuitous b.^[17] Wolfgang Schramm has shown that

\gcd(a,b)=\sum \limits _{k=1}^{a}\exp(2\pi ikb/a)\cdot \sum \limits _{d\left|a\right.}{\frac {c_{d}(k)}{d}}

is an entire part in the variable b for all positive integers a where c _d(thousand) is Ramanujan'southward sum.^[18]

Complication [edit]

The computational complexity of the computation of greatest common divisors has been widely studied.^[19] If one uses the Euclidean algorithm and the simple algorithms for multiplication and division, the computation of the greatest mutual divisor of two integers of at most $n$ bits is $O(due north^{2}).$ This means that the computation of greatest common divisor has, upwardly to a abiding factor, the same complexity as the multiplication.

However, if a fast multiplication algorithm is used, one may alter the Euclidean algorithm for improving the complexity, but the computation of a greatest mutual divisor becomes slower than the multiplication. More precisely, if the multiplication of two integers of $northward$ bits takes a time of $T (north)$ , then the fastest known algorithm for greatest common divisor has a complexity $O\left(T(n)\log due north\right).$ This implies that the fastest known algorithm has a complexity of $O\left(n\,(\log n)^{2}\right).$

Previous complexities are valid for the usual models of computation, specifically multitape Turing machines and random-admission machines.

The ciphering of the greatest common divisors belongs thus to the course of issues solvable in quasilinear time. A fortiori, the corresponding determination problem belongs to the class P of problems solvable in polynomial fourth dimension. The GCD problem is not known to be in NC, then there is no known way to parallelize information technology efficiently; nor is it known to be P-complete, which would imply that it is unlikely to be possible to efficiently parallelize GCD computation. Shallcross et al. showed that a related problem (EUGCD, determining the residuum sequence arising during the Euclidean algorithm) is NC-equivalent to the problem of integer linear programming with two variables; if either trouble is in NC or is P-complete, the other is as well.^[20] Since NC contains NL, it is likewise unknown whether a infinite-efficient algorithm for computing the GCD exists, even for nondeterministic Turing machines.

Although the problem is non known to exist in NC, parallel algorithms asymptotically faster than the Euclidean algorithm exist; the fastest known deterministic algorithm is past Chor and Goldreich, which (in the CRCW-PRAM model) can solve the trouble in $O (n /log north)$ fourth dimension with $north i+ε$ processors.^[21] Randomized algorithms can solve the problem in $O ((log due north) two)$ fourth dimension on $\exp \left(O\left({\sqrt {n\log n}}\right)\right)$ processors^{[ description needed ]} (this is superpolynomial).^[22]

Properties [edit]

Every mutual divisor of a and b is a divisor of gcd(a, b).
gcd(a, b), where a and b are non both aught, may be defined alternatively and equivalently equally the smallest positive integer d which can be written in the form d = a⋅p + b⋅q , where p and q are integers. This expression is called Bézout'south identity. Numbers p and q like this can be computed with the extended Euclidean algorithm.
gcd(a, 0) = | a |, for a ≠ 0, since any number is a divisor of 0, and the greatest divisor of a is | a |.^[two] ^[5] This is usually used as the base of operations instance in the Euclidean algorithm.
If a divides the production b⋅c, and gcd(a, b) = d , so a/d divides c.
If one thousand is a positive integer, and then gcd(m⋅a, m⋅b) = m⋅gcd(a, b).
If grand is any integer, then gcd(a + k⋅b, b) = gcd(a, b). Equivalently, gcd(a mod b,b) = gcd(a,b).
If k is a positive mutual divisor of a and b, so gcd(a/m, b/yard) = gcd(a, b)/m .
The GCD is a commutative function: gcd(a, b) = gcd(b, a).
The GCD is an associative function: gcd(a, gcd(b, c)) = gcd(gcd(a, b), c). Thus gcd(a, b, c, ...) can be used to announce the GCD of multiple arguments.
The GCD is a multiplicative function in the post-obit sense: if a _one and a ₂ are relatively prime, then gcd(a _one⋅a ₂, b) = gcd(a ₁, b)⋅gcd(a ₂, b).
gcd(a, b) is closely related to the to the lowest degree common multiple lcm(a, b): nosotros have

gcd(a, b)⋅lcm(a, b) = | a⋅b |.

This formula is often used to compute to the lowest degree mutual multiples: one first computes the GCD with Euclid's algorithm and and so divides the product of the given numbers past their GCD.

The following versions of distributivity hold true:

gcd(a, lcm(b, c)) = lcm(gcd(a, b), gcd(a, c))

lcm(a, gcd(b, c)) = gcd(lcm(a, b), lcm(a, c)).
If we have the unique prime factorizations of a = p ₁ ^{east _one} p ₂ ^{e ₂} ⋅⋅⋅ p _m ^{e _m} and b = p ₁ ^{f ₁} p ₂ ^{f ₂} ⋅⋅⋅ p _m ^{f _yard} where e_i ≥ 0 and f_i ≥ 0 , then the GCD of a and b is

gcd(a,b) = p ₁ ^{min(e ₁,f _one)} p ₂ ^{min(e _ii,f ₂)} ⋅⋅⋅ p _grand ^{min(due east _k,f _m)} .
It is sometimes useful to define gcd(0, 0) = 0 and lcm(0, 0) = 0 because then the natural numbers become a complete distributive lattice with GCD equally meet and LCM as join performance.^[23] This extension of the definition is likewise compatible with the generalization for commutative rings given beneath.
In a Cartesian coordinate arrangement, gcd(a, b) can exist interpreted equally the number of segments between points with integral coordinates on the direct line segment joining the points (0, 0) and (a, b).
For non-negative integers a and b, where a and b are not both zip, provable past considering the Euclidean algorithm in basedue north:^[24]

gcd(n ^a − ane, due north ^b − 1) = n ^gcd(a,b) − 1.
An identity involving Euler'due south totient function:

$\gcd(a,b)=\sum _{k|a{\text{ and }}thousand|b}\varphi (m).$
$\sum _{chiliad=1}^{northward}\gcd(k,n)=n\prod _{p|n}\left(one+\nu _{p}(north)\left(1-{\frac {i}{p}}\correct)\right)$ where $\nu _{p}(due north)$ is the p-adic valuation.

Probabilities and expected value [edit]

In 1972, James Eastward. Nymann showed that thousand integers, chosen independently and uniformly from {i, ...,north}, are coprime with probability 1/ζ(thousand) as due north goes to infinity, where ζ refers to the Riemann zeta part.^[25] (See coprime for a derivation.) This result was extended in 1987 to show that the probability that k random integers have greatest common divisor d is d ^−grand/ζ(k).^[26]

Using this information, the expected value of the greatest common divisor role can be seen (informally) to not exist when yard = two. In this case the probability that the GCD equals d is d ⁻ⁱⁱ/ζ(2), and since ζ(two) = π²/half dozen nosotros have

\mathrm {E} (\mathrm {two} )=\sum _{d=1}^{\infty }d{\frac {6}{\pi ^{2}d^{2}}}={\frac {6}{\pi ^{2}}}\sum _{d=1}^{\infty }{\frac {1}{d}}.

This concluding summation is the harmonic serial, which diverges. However, when 1000 ≥ 3, the expected value is well-defined, and past the higher up argument, it is

\mathrm {East} (k)=\sum _{d=ane}^{\infty }d^{one-k}\zeta (k)^{-ane}={\frac {\zeta (k-1)}{\zeta (yard)}}.

For k = 3, this is approximately equal to 1.3684. For k = 4, it is approximately one.1106.

In commutative rings [edit]

The notion of greatest common divisor tin more than mostly exist divers for elements of an arbitrary commutative band, although in general there demand non be one for every pair of elements.

If $R$ is a commutative band, and $a$ and $b$ are in $R$ , and so an element $d$ of $R$ is chosen a common divisor of $a$ and $b$ if it divides both $a$ and $b$ (that is, if in that location are elements $x$ and $y$ in $R$ such that d·x =a and d·y =b). If $d$ is a mutual divisor of $a$ and $b$ , and every common divisor of $a$ and $b$ divides $d$ , then $d$ is called a greatest mutual divisor of $a$ and b.

With this definition, two elements $a$ and $b$ may very well have several greatest common divisors, or none at all. If $R$ is an integral domain and so any two GCD's of $a$ and $b$ must exist associate elements, since past definition either 1 must divide the other; indeed if a GCD exists, any one of its associates is a GCD likewise. Beingness of a GCD is not assured in arbitrary integral domains. However, if $R$ is a unique factorization domain, so whatever 2 elements have a GCD, and more generally this is true in GCD domains. If $R$ is a Euclidean domain in which euclidean division is given algorithmically (as is the case for instance when R = F[X] where $F$ is a field, or when $R$ is the ring of Gaussian integers), and then greatest common divisors can be computed using a grade of the Euclidean algorithm based on the division procedure.

The following is an case of an integral domain with ii elements that do non have a GCD:

R=\mathbb {Z} \left[{\sqrt {-3}}\,\,\correct],\quad a=4=2\cdot 2=\left(1+{\sqrt {-iii}}\,\,\correct)\left(one-{\sqrt {-three}}\,\,\right),\quad b=\left(1+{\sqrt {-3}}\,\,\correct)\cdot 2.

The elements two and i +√−3 are two maximal mutual divisors (that is, any common divisor which is a multiple of ii is associated to two, the same holds for one +√−3 , but they are non associated, so there is no greatest common divisor of $a$ andb.

Corresponding to the Bézout property we may, in whatsoever commutative ring, consider the collection of elements of the form pa +qb, where $p$ and $q$ range over the ring. This is the ideal generated by $a$ and $b$ , and is denoted simply (a,b). In a ring all of whose ideals are principal (a principal ideal domain or PID), this ideal will be identical with the prepare of multiples of some ring element d; and then this $d$ is a greatest mutual divisor of $a$ and b. But the ideal (a,b) can be useful even when in that location is no greatest mutual divisor of $a$ and b. (Indeed, Ernst Kummer used this ideal as a replacement for a GCD in his handling of Fermat's Last Theorem, although he envisioned it as the set of multiples of some hypothetical, or ideal, ring element $d$ , whence the band-theoretic term.)

See too [edit]

Bézout domain
Lowest common denominator
Unitary divisor

Notes [edit]

^ ^a ^b Long (1972, p. 33)
^ ^a ^b ^c Pettofrezzo & Byrkit (1970, p. 34)
^ Kelley, West. Michael (2004), The Complete Idiot's Guide to Algebra, Penguin, p. 142, ISBN9781592571611 .
^ Jones, Allyn (1999), Whole Numbers, Decimals, Percentages and Fractions Year 7, Pascal Press, p. xvi, ISBN9781864413786 .
^ ^a ^b ^c Hardy & Wright (1979, p. xx)
^ Some authors care for greatest common denominator equally synonymous with greatest common divisor. This contradicts the mutual pregnant of the words that are used, as denominator refers to fractions, and ii fractions do not accept any greatest mutual denominator (if two fractions take the same denominator, one obtains a greater mutual denominator past multiplying all numerators and denominators by the same integer).
^ Barlow, Peter; Peacock, George; Lardner, Dionysius; Airy, Sir George Biddell; Hamilton, H. P.; Levy, A.; De Morgan, Augustus; Mosley, Henry (1847), Encyclopaedia of Pure Mathematics, R. Griffin and Co., p. 589 .
^ Some authors use $(a, b)$ ,^[1] ^[2] ^[5] only this note is often ambiguous. Andrews (1994, p. sixteen) explains this as: "Many authors write (a,b) for $yard.c.d.(a, b)$ . Nosotros do not, because we shall often utilize (a,b) to represent a point in the Euclidean aeroplane."
^ Thomas H. Cormen, et al., Introduction to Algorithms (2nd edition, 2001) ISBN 0262032937, p. 852
^ Bernard L. Johnston, Fred Richman, Numbers and Symmetry: An Introduction to Algebra ISBN 084930301X, p. 38
^ Martyn R. Dixon, et al., An Introduction to Essential Algebraic Structures ISBN 1118497759, p. 59
^ e.g., Wolfram Alpha adding and Maxima
^ Jonathan Katz, Yehuda Lindell, Introduction to Modern Cryptography ISBN 1351133012, 2020, department 9.one.ane, p. 45
^ Weisstein, Eric W. "Greatest Common Divisor". mathworld.wolfram.com . Retrieved 2020-08-30 .
^ "Greatest Common Factor". world wide web.mathsisfun.com . Retrieved 2020-08-thirty .
^ Gustavo Delfino, "Understanding the To the lowest degree Mutual Multiple and Greatest Common Divisor", Wolfram Demonstrations Projection, Published: February ane, 2013.
^ Slavin, Keith R. (2008). "Q-Binomials and the Greatest Mutual Divisor". INTEGERS: The Electronic Journal of Combinatorial Number Theory. University of W Georgia, Charles University in Prague. 8: A5. Retrieved 2008-05-26 .
^ Schramm, Wolfgang (2008). "The Fourier transform of functions of the greatest mutual divisor". INTEGERS: The Electronic Journal of Combinatorial Number Theory. University of West Georgia, Charles University in Prague. 8: A50. Retrieved 2008-eleven-25 .
^ Knuth, Donald E. (1997). The Art of Computer Programming. Vol. two: Seminumerical Algorithms (3rd ed.). Addison-Wesley Professional. ISBN0-201-89684-2.
^ Shallcross, D.; Pan, Five.; Lin-Kriz, Y. (1993). "The NC equivalence of planar integer linear programming and Euclidean GCD" (PDF). 34th IEEE Symp. Foundations of Computer science. pp. 557–564.
^ Chor, B.; Goldreich, O. (1990). "An improved parallel algorithm for integer GCD". Algorithmica. 5 (1–four): 1–x. doi:10.1007/BF01840374. S2CID 17699330.
^ Adleman, Fifty. M.; Kompella, K. (1988). "Using smoothness to achieve parallelism". 20th Annual ACM Symposium on Theory of Calculating. New York. pp. 528–538. doi:ten.1145/62212.62264. ISBN0-89791-264-0. S2CID 9118047.
^ Müller-Hoissen, Folkert; Walther, Hans-Otto (2012), "Dov Tamari (formerly Bernhard Teitler)", in Müller-Hoissen, Folkert; Pallo, Jean Marcel; Stasheff, Jim (eds.), Associahedra, Tamari Lattices and Related Structures: Tamari Memorial Festschrift, Progress in Mathematics, vol. 299, Birkhäuser, pp. 1–twoscore, ISBN9783034804059 . Footnote 27, p. 9: "For instance, the natural numbers with gcd (greatest mutual divisor) as see and lcm (to the lowest degree common multiple) as bring together operation determine a (complete distributive) lattice." Including these definitions for 0 is necessary for this issue: if one instead omits 0 from the set of natural numbers, the resulting lattice is not complete.
^ Knuth, Donald E.; Graham, R. L.; Patashnik, O. (March 1994). Concrete Mathematics: A Foundation for Calculator Science. Addison-Wesley. ISBN0-201-55802-5.
^ Nymann, J. Due east. (1972). "On the probability that k positive integers are relatively prime". Journal of Number Theory. 4 (5): 469–473. Bibcode:1972JNT.....4..469N. doi:x.1016/0022-314X(72)90038-8.
^ Chidambaraswamy, J.; Sitarmachandrarao, R. (1987). "On the probability that the values of m polynomials accept a given thousand.c.d." Journal of Number Theory. 26 (3): 237–245. doi:x.1016/0022-314X(87)90081-3.

References [edit]

Andrews, George Eastward. (1994) [1971], Number Theory, Dover, ISBN9780486682525
Hardy, G. H.; Wright, Eastward. Thou. (1979), An Introduction to the Theory of Numbers (Fifth ed.), Oxford: Oxford University Press, ISBN978-0-19-853171-5
Long, Calvin T. (1972), Elementary Introduction to Number Theory (2nd ed.), Lexington: D. C. Heath and Company, LCCN 77171950
Pettofrezzo, Anthony J.; Byrkit, Donald R. (1970), Elements of Number Theory, Englewood Cliffs: Prentice Hall, LCCN 71081766